AMI: Agent for Music Inscrtiption

AMI (pronounced "Amy"), is an agent that writes music. This software composes short musical pieces, in a simple but interesting style.

The rest of this document will cover the following aspects of AMI:

  1. Domain
  2. Illustration
  3. Hear Music
  4. Methods
  5. Source Code
  6. Conclusions
  7. Future-Plans
Domain

By definition, an agent is an AI program that acts in a domain. AMI's domain is the world of music. For my purposes this is a two-dimensional world. The set of dimensions of AMI's domain can be thought of as a tuple:

Domain = {pitch, rhythm}

This domain is represented in Prolog in the following structure: 

staff(Note,Rhythm)

Such that Note represents a note and Rhythm represents a rhythm. These variables can take on the following values:

Note can be {a,a#,b,c,c#,d,d#,e,f,f#,g,g#}

Rhythm can be {4,5,8,12,16}

(meaning: quarter note, dotted quarter note, eighth note, dotted eighth note, sixteenth note)

A list of these structures can be seen as a piece of music. For example:

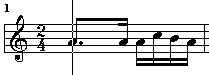Music on a staff

Could be seen as: 

[staff(a,12), staff(a,16), staff(a,16), 
 staff(c,16), staff(b,16), staff(a,16)]

With these structures AMI can write music, and her output can be in the above form.

Illustration

A typical session with AMI from the user's point of view is the following:

  1. Start Prolog and load AMI.
  2. Type a query of the following form: 
    go(c-sharp,16).

    This asks AMI to write a piece of music in the key of c-sharp minor that is sixteen bars long. (All of AMI's music is in a minor key because that is the type of music that I like best).

  3. AMI will then write a piece of music on the screen in the form of a list.
  4. The user will then read the output and manually convert it to a musical staff, as described in the Domain above.
  5. At this point the user should play what is on the staff. If the user wants more music, he can ask AMI another query, in the same form of the above, and she will write a different piece of music.

The following is a text file of one of my sessions with AMI, as well as what the music looks like from the session, after I converted the output to a staff:

I recorded the music from this session on my guitar. AMI writes music that will fit a chord progression. She also prints this progression along with her music. In the recording, there are three guitars. One of them simply strums each chord from the progression, and is in the background of the mix. In this particular session I asked AMI to come up with a 32 bar piece. One guitar plays all of the even bars (2,4,...,32) and the other guitar plays the odd bars (1,3,...,31). This allows for a "call-response" style. (Keep in mind that it was not AMI's idea to perform the piece this way, such performance decisions are outside of her domain). The recordings of myself playing music from this session are below.

Methods

There are four main problems to solve to make an agent like AMI:

  1. Come up with a chord progression
  2. Come up with a motif that implies any chord
  3. Transform any motif so that it implies any chord in any progression
  4. Apply music theory to do the above three.

I will address these problems in reverse order, since Problem Four's solution will be the basis of solving the others.

Solving Problem Four

In order to solve the first three problems, AMI needs to have some basic knowledge of music theory. The basis of much of the harmonic aspects of music theory rely on intervals, i.e. the distance between notes. Musicians have different names for these intervals, that are given relative to a scale. I formalized the eleven intervals of the chromatic scale, so that any particular interval could be called relative to a root note (of any key). The following is an example query: 

minor_third(g-sharp, X)

to which AMI would reply that X = b, since b is the minor third of g sharp.

I then formalized the chord-scales in a similar way. Chord scales are how musicians look at a chord progression of a piece in a general way. They are scales, which in this case are harmonized to make up a three note chord.

Solving Problem Three

We can use AMI's music theory predicates and the representations described in the domain to write a new predicate that will transform a motif that implies one chord from a progression, to make it imply another chord in the same progression. The approximate algorithm to do this is the following:

  1. Remove the head of the list (i.e.take the first note of the motif). The head will be a staff structure, which has a harmonic and rhythmic aspect.
  2. Make a new staff structure N to be the head for the new motif list.
  3. Set N to have the same rhythm as the note of the head of the original list.
  4. To set the harmonic aspect of N use the chord that the original motif was trying to imply, and compute the interval I1 between that chord and the note in the head. Then use the same I1 with respect to the chord that N is trying to imply, to set N.
  5. Recurse until the original list is empty.

The above algorithm will make a new motif, that implies a different chord, as specified by the progression. This new motif will keep the same rhythm and melodic contour. There are additional features that are done to keep the transformations diatonic, but an explanation of this would bring about a long discussion. These relationships are formalized in the predicate called next, and can been examined in the source code below.

Solving Problem Two

Problem Two requires that this agent be somewhat autonomous. Her goal is to write a motif. We will consider two ways to look at what writing a motif means:

  1. AMI is going to write a motif that will be the musical heart and soul of the piece of music she will compose.
  2. AMI is going to generate some random numbers, to be used with a few simple rules that I came up with, to generate a list of staff structures.

It is my hope that the first view will be taken by the listener, who hears the form of the music and chooses to attribute meaning to it in an artistic way. The second view presents a reasonable challenge to a programmer. The most intuitive requirement for a satisfactory motif is that there be some type of human spontaneity. The best way to simulate this in a computer is to use a random number generator. I will now explain some of the code that AMI uses to generate a motif.

The following predicate m, specifies a relation of a motif, List: 

m(chord(X,minor), List):- 
    rm(L), rn(chord(X,minor), L, List),

rm is true if L is a rhythmic motif, i.e. L is a list of numbers, such that those numbers represent rhytmic values, as mentioned in the domain discussion above. rn is true if List is a motif, i.e. List is a list of staff structures. The rhythmic values of these staff structures must have the same values as L, and the harmonic values can only be notes from the X-minor scale.

rm is defined in terms of a set of random numbers n, whose range is from one to four. Another set of random numbers are used to determine which rhythmic value (quarter note, dotted quarter note, eighth note, sixteenth note) will be selected, and this rhythmic value will be repeated n times. This entire procedure will occur recursively, with a randomly picked recursion depth of r, such that 0 < r < 5. The procedure will generate a motif of ultimately random length and random time signature, that will be maintained for the entire piece.

The rhythmic motif is generated this way because it imitates a common paradigm of music; repetition. Most motifs repeat a rhythmic value between one and four times, before switching to a new rhythmic value. The other important feature of music is that these rhythms seem to be chosen in no particular order, so again I used random numbers.

The predicate rn gives a harmonic aspect to the rhythmic motif, that implies a particular chord. The general rule in this case is the following. A three note chord (the type AMI works with) has a seven note scale, and a motif will imply that chord, just in case its notes are contained within that scale. This rule is satisfied by rn because rn will randomly select only the notes that are within the scale of the chord that it is trying to imply.

Solving Problem One

If this final problem is solved, AMI will be able come up with a chord progression. This problem also requires AMI to be somewhat autonomous, so random numbers will again play an important role. In this case the challenge is met by using the metaphor of a search problem. The predicate cruel_world defines the next point in the search space relative to the key of the piece. AMI must search through the cruel world to find what chord she will play next. The reasoning behind the title of this predicate will be discussed later.

In the common seven note scale found in almost all of western music, there are seven chords, based on the scale of the key, also known as the root. These seven chords are usually written in roman numerals, such that upper case numerals indicate major chords, and lower case numerals indicate minor chords. Each of these chords generate feelings of tension and resolution in the average listener. The degree of tension or resolution that these chords can make the average listener feel have traditionally been separated into three categories, which I have listed below, in order of increasing dissonance: 

Tonic:         I
Dominant:      V, vii
Pre-Dominant:  ii, IV, vi

AMI searches the cruel world for the Tonic, so that the piece of music can resolve, but the odds of her finding it are not in her favor. Hence the name of the predicate that represents the search space is "cruel world". She sometimes finds a Dominant chord so that the listener feels a partial resolution, but most of the time she finds Pre-Dominant chords. This keeps the piece of music interesting and gives the listener a sense of adventure. A good analogy to this idea is to imagine a story in which the main character lives a happy life and is never challenged. The average person would find this story boring in comparison to one in which the main character starts out being happy (all of AMI's pieces start on the Tonic), faces some challenges (Pre-Dominant chords), achieves partial success (Dominant chords), and then in the end achieves total success and resolution (the Tonic).

This search problem was implemented with the predicate cruel_world, which uses random numbers ranging from 1 to 6. This predicate will only be true 1/6 of the time if the next chord is the Tonic. It will also only be true 1/3 of the time if the next chord is the Dominant, and the other half of the time it will be true if the next chord is the Pre-Dominant. This scheme was implemented with a random number generator and some formalizations of these sets of chords.

The cruel world is not such a bad place for AMI, when she uses a little bit of planning. This planning becomes relevant to coming up with a good chord progression, because such a chord progression should use a cadence to end on the tonic. A cadence is a set of chords that end a piece so that it resolves. You can read more about them, as well as some of the relations that I formalized at:

http://dspace.dial.pipex.com/andymilne/Cadentialprog.shtml

Any effective cadence must contain at least three chords, if the progression has only triads (the kinds of progressions AMI will be writing). This means that AMI will have to plan on how to end the progression using the following idea. If a piece of music is n bars long, then at bar k, where k = n - 3, AMI will leave the cruel word and finish the progression by randomly choosing, with equal probability, one of the following six cadences. 

(b = flat)
1.  v - iv - i
2.  bVII - iv - i
3.  bVI - bVII - i
4.  iv - bVII - i
5.  bVI - v - i
6.  iv - v - i

For this reason the cruel world search space always has a consonant ending.

Download the source code in Prolog here.

Conclusions

Creating AMI taught me more about Artificial Intelligence, as well as Music. I will now discuss this project's impact in both areas.

This project makes one question what it means to compose a piece of music. One of my main criticisms of my program is that it is lacking an important element that goes into the composition of a piece. The average human composer might go through a process like the following:

  1. Improvise in a certain key (this could be a structured but random process that is similar to what AMI does).
  2. Decide if he likes what he hears, and then go back to step one, or write down what he has improvised, for further variation.

There are many other ways to look at Composition, but I feel that the above process really touches the essential elements. Many composers claim to have some a type of auditory image or "vibe" that they are pursuing, but this aspect is captured in step two.

I am satisfied with my project with regard to abstracting some rules to capture step one, and then formalizing these rules in Prolog. However, I feel that the user has to take care of step two. For example, In my interactions with AMI I played some of the things she wrote and decided that they were not good, so I queried her to write another piece.

This limitation of AMI worth noting. She is useful in that she will compose a piece of music, but she is not completely autonomous. She will not know if the music that she composed is any good. The rules that I abstracted to implement step one, try to set things so that AMI will compose a good piece of music, but I don't believe that even humans know exactly what combination of rhythms and notes will always make good music. People seem to experiment as in step one, and then listen, as in step two. The rule that I found in trying to capture step one is very loose. The rule is that there simply are combinations of rhythms that should vary, and that these notes tend to come from a scale that implies a specific key (even if the key happens to be atonal, the notes will have to come from the chromatic scale).

One way to solve this problem is to write another agent that specializes in listening to music. This agent could then be set up to work with AMI, such that the new agent will reject the pieces that AMI writes, that it does not like. These two agents could be combined into a more sophisticated agent for music inscription. An even better advancement would involve giving AMI the ability to learn, and then giving the listening agent the ability to teach. I could then let the two agents work together for some time, and come back to find much better music being made.

Future Plans

AMI's interface is somewhat limiting with regard to how a user asks AMI a question and what the user can do with her answer.

Input

I would like to configure a CGI so that users can then ask AMI to generate music over the web. The main predicate for AMI is "go": 

go(Key, Bars).

I would like to create a simple online form so that both Key and Bars can be input through a GUI over the web.

Output

AMI's staff based lists which come from Prolog are not difficult to read but are non-standard: 

[staff(a,12), staff(a,16), staff(a,16), 
staff(c,16), staff(b,16), staff(a,16)]

I would like to create a script which can parse the output to convert it into notation. I am also interested in a script that might be able to convert the above Prolog list into a format which would allow it to be heard immediately (perhaps MIDI).