Mathematical Functions

In the first quarter of this class we talked about functions. Functions are very important. They allow a programmer to simplify a large and complicated program into a set of small and simple programs. As we learned, a lot of those small and simple programs are already written for you, and you just need to be able to look them up to put them to use.

It is helpful to think of a function as a black box. By this I mean that you need no knowledge of how a function was implemented. You just need to know what it takes as input, and returns as output so that you can use it to get your job done. For example, when you use your calculator to add two numbers you don't bother questioning how the calculator added the numbers, you simply use the calculator to get the answer you are interested in. If you were interested in calculator design the black box paradigm might not be the case when applied to this particular use of the calculator, but even the calculator builder, would use the black box paradigm at some level. For any complicated system that you have to design you can first build a working basis and then ignore the details of the basis, so that you can again focus on the system itself.

We are now going to study some mathematical functions. The first set of functions that we are going to be using can be found in the PHP Manual's entry on Mathematical Functions. One of the first things that come up in the PHP manual is a mention of integers and floats. These are different types of numbers that PHP will support. The distinction between these types is very important for languages such as C and Java, but in PHP making the distinction is less important. For the purposes of this tutorial an integer is any number of the following set:

Z = {..., -2, -1, 0, 1, 2, ...}

For the purposes of this tutorial, the set of floats will refer to a subset (because they are computed in a finite computer) of the numbers that are known in the set of real numbers. For example 2.5 or 10001.2. It would be difficult to enumerate the set of floats as I did above for the integers. (It is impossible to enumerate the set of reals.)

Using Existing Math Functions

One PHP Math function which can be fun to use is rand which generates random numbers. Since HTML represents colors as numbers you can use this function to create a page with random colors like this one (If you click reload a few times the background color should change. Rand is not truly random so please be patient).

Let's have a look at the code for the random color page:

function random_color() 
{
  $rd = rand(0, 255);
  $gd = rand(0, 255);
  $bd = rand(0, 255);

  $rh = dechex($rd);
  $gh = dechex($gd);
  $bh = dechex($bd);

  return "$rh$gh$bh";
}

$color = random_color();
print "<body bgcolor=\"$color\">";
print "<h2>This page has random colors</h2>";

In the above a function called random_color() is defined which returns a random hexadecimal string. Random hexadecimal strings are useful in this case since HTML colors can be specified with hexadecimal numbers.

The function generates three numbers, each of which range between 0 and 255 (since HTML allows for 256 shades of a color). The three numbers correspond to a the vector {R, G, B}. The variables are labeled {$rd, $gd, $bd} to show their relation to that vector and they were labeled $rd as opposed to $r to specify that they are decimal numbers i.e. base 10, the number system that most people count with ranging from 0 to 9. The three decimal numbers are then converted to hexadecimal numbers (base 16, ranging from 0 to f) by the function dechex. The random hexadecimal string is then returned from the function call and then displayed as the page's background color.

PHP has a variety of Math functions which come in handy. In general they cover the following areas:

Trigonometric Functions
Base Conversion Functions
Logarithmic Functions
Exponential Functions
Random Number Functions
Functions for computing Max, Min, Floor, and Ceiling

Recursion

This final example demonstrates that PHP supports recursion for the sake of completeness. Understanding how to use and define your own functions is essential to this course but understanding recursive functions is not. However, you might encounter recursive functions in the future, and they are a very powerful construct for any language.

Recursion means defining something in terms of itself. We will study recursion by looking at a classic example. Do you see a pattern in the following numbers?

1, 1, 2, 3, 5, 8, 13, 21, ...

If you look at the above series, you should notice that each number is the sum of the previous two. i.e.:

1 + 1 = 2 first + second = third

1 + 2 = 3 second + third = fourth

2 + 3 = 5 third + fourth = fifth

3 + 5 = 8 fourth + fifth = sixth

5 + 8 = 13 fifth + sixth = seventh

8 + 13 = 21 sixth + seventh = eighth

... ...

This simple series is called "the Fibonacci numbers" it has some very interesting properties. How would we write a PHP script to produce these numbers?

Suppose that we could use the variable n to refer to any number in the above sequence, such that if n referred to the sixth number, then n-1 would refer to the fifth, and n-2 would refer to the fourth. We could then have a function F(n) such that it would return the nth number from the series. Since the nth number is defined as the sum of the previous two, and since the previous two numbers would be denoted by n-1 and n-2 respectively, we could say the following:

F(n) = F(n-1) + F(n-2)

which is a more formal way of saying that one number is the sum of the previous two. The above could pick out all of the Fibonacci numbers with the exception of the first two, so we have to make an exception to our function above. This results in the following:

F(n) = 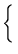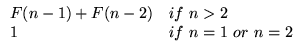F(n) = F(n-1) + F(n-2) if n > 2 OR 1 if n = 1 or n = 2

The above exception that we have made is very important, since it covers the base case, in other words how the series starts. If our exception rule had been different the above would not produce the right numbers. The most important part of our exception rule is that it allows us to eventually find a Fibonacci number. By this I mean that to find one Fibonacci we search for its previous numbers and continue to go back further until we find ourselves asking for the first and second number. When we get to this point, we can no longer search for these numbers in terms of themselves, so they have to be defined directly. We can then build any number we are looking for from the first and second number.

We can convert the above definition into PHP quite easily. In the following we define a function called fib($n) which will return the $nth Fibonacci number. There is also a loop to call this function to produce the first ten Fibonacci numbers and echo the results:

function fib($n) {
  if (($n == 1) or ($n == 2))
       	return 1; 
  if ($n > 2) 
	return fib($n-1) + fib($n-2);
} 

for($i = 1; $i <= 10; $i++) {
  $fib = fib($i);
  echo "$fib<br>"; 
}

To run the above code click here. (There are faster ways to compute Fibonacci numbers but that is beyond the scope of this class. The curious can search the web for better methods.)

Notice that fib() contains calls to itself, and thus it is a recursive function. It is important when defining these types of functions to have a case where the function does not call itself. If you don't do this then your program will never stop executing.

Here are some general rules to help you define a recursive function:

Always change at least one argument while recurring.
Always have a condition which will stop the recursion based on the changed argument.
When recurring on a number always ask if the number is zero or one.

The goal of our next practice is to get you to use the tools that we have learned since day one in a new way. There will also be an extra credit part of the next practice which requires recursion.

jfulton [at] member.fsf.org
22 Aug 2013